Similar to Decision Tree model induction, Random Forest induction is also a classification modeling type. Just as a forest has many trees, Random Forests can be considered a collection of Decision Tree algorithms. The advantage of an ensemble learning algorithm such as Random Forest is that each tree is built by injecting some randomness into the tree generating procedure. The resulting model is then generated from the n amount of trees (n = 10 in this case).

I will be using the now familiar creditcard.csv file. Initially downloaded from Kaggle, this dataset contains credit card transactions made over two days in September 2013. Over this period, we have 492 frauds out of 284,807 transactions. The dataset is highly unbalanced, as the positive class (frauds) account for only 0.172% of all transactions. The target (fraud) variable is indicated by the field “Class”

Start by importing the necessary libraries.

Import the data, specify the dependent (target) and independent variables

Split the dataset into a training and testing dataset. This way we can test the accuracy of the model later on.

Create the Random Forest model

Create and plot a confusion matrix, and calculate model accuracy

The confusion matrix has two axes. A “true” axis and a “predicted” axis. We have 112 instances where the True and Predicted labels indicate a fraudulent transaction. The model predicted a fraud, and there was an actual fraud. There were 71,044 instances where the model predicted “No Fraud” and there was actually no fraudulent transactions.

The overall accuracy of the model can be calculated as (71,044 + 112) / (71,044 + 112 + 9 + 37) = 99.94%  At first glance, this sounds great, but we only have 149 fraudulent transactions out of a total of 71,202. Thus our base accuracy rate, if we classified every transaction as “no fraud,” would be 99.79%

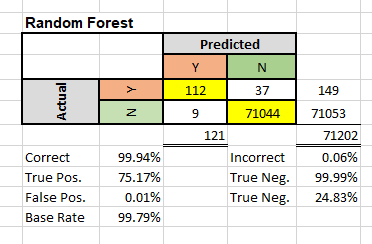
More importantly, would be the false positive and true positive accuracy. Without a model, if we classified every transaction as “non-fraudulent”, we would have an overall accuracy of 99.79%, but a False Positive and True Positive rate of 0%

Using a model, we have 37 instances where the model predicted a fraudulent transaction, but there were no frauds (false positive rate of 0.01%). For the true positive rate, we have 112 instances where the model predicted a fraudulent transaction, which was in fact fraudulent. This would give us a true positive rate of 75.17%. (112 / (112+37)).

As expected, this is the best positive fraud detection rate from all the models tried thus far. The downside of using an ensemble model is the time that it takes to run.